Spherical Harmonics In Gaussian Splats
🔸 Why Use Spherical Harmonics in Gaussian Splats?
When rendering 3D scenes using Gaussian splats, each point (or “splat”) needs to represent not just color, but how that color changes depending on the viewing direction. Spherical harmonics allow encoding this angular variation compactly.
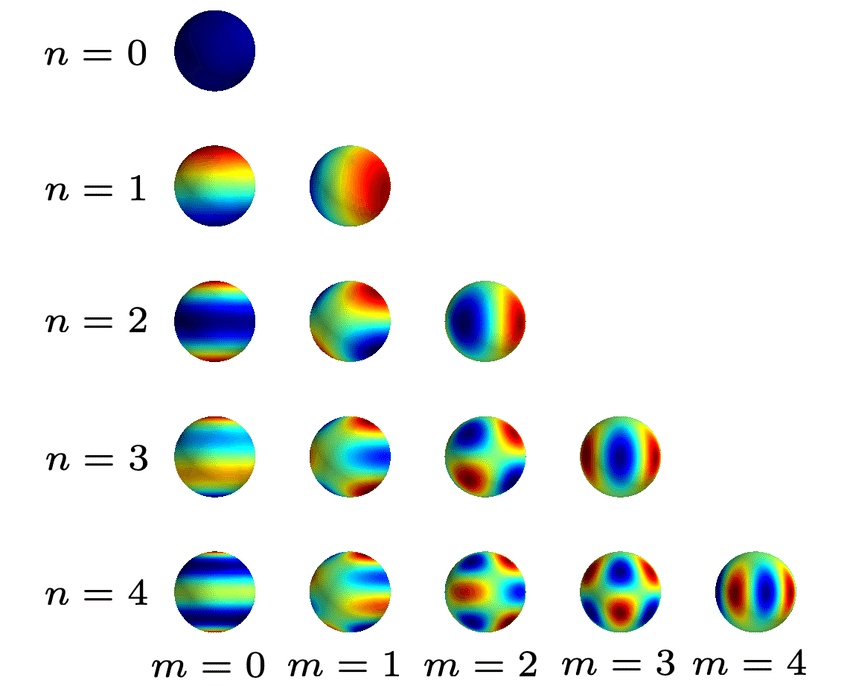
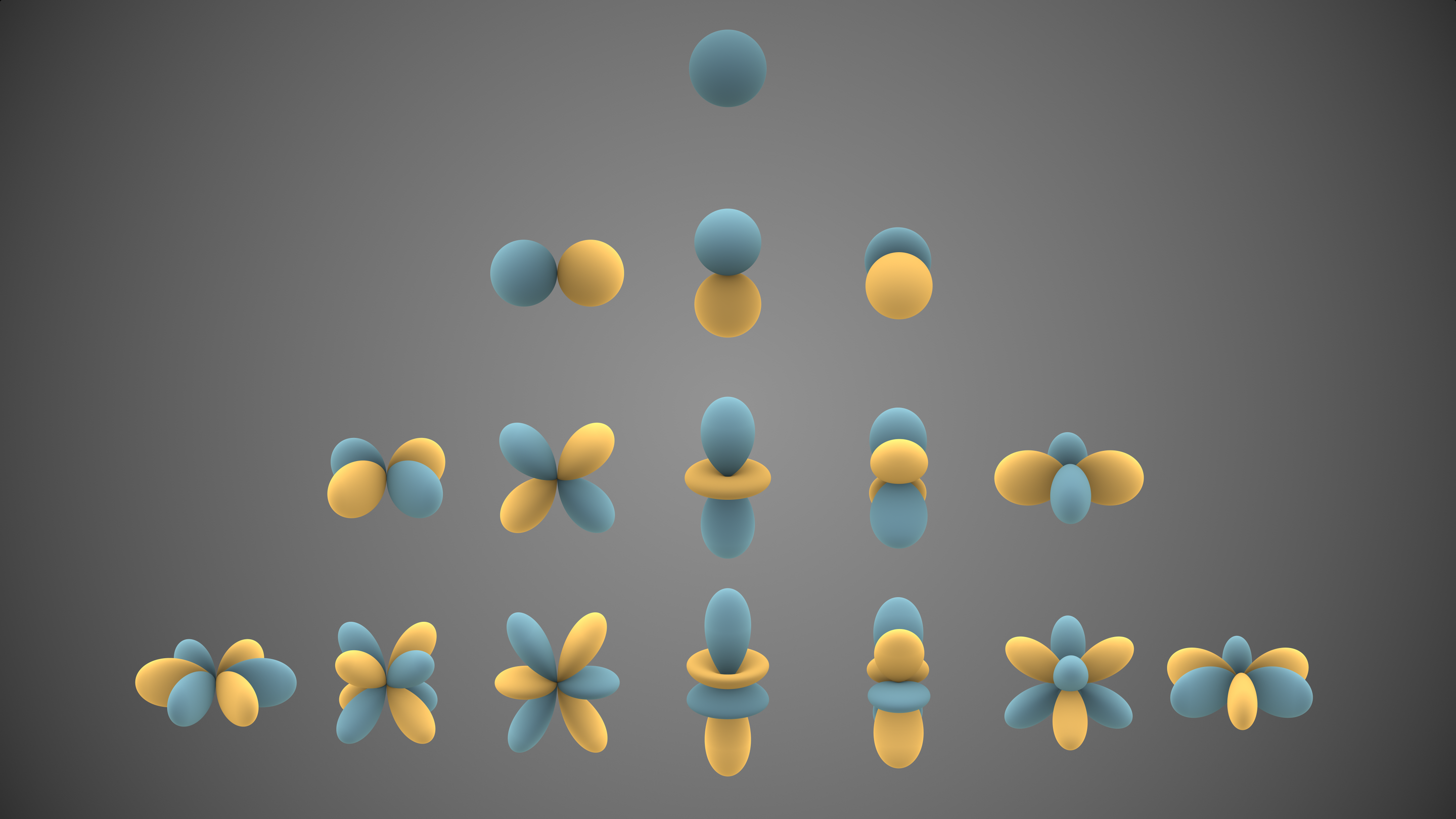
Left: Spherical harmonics mapped to a sphere | Right: Spherical harmonics visualization
This is important for achieving photorealistic rendering with effects like:
- Specular highlights
- Soft shadows
- View-dependent lighting changes
🔸 What Are Spherical Harmonics?
Spherical Harmonics (SH) are a series of orthogonal basis functions defined on the surface of a sphere. You can think of them as the 3D analog of Fourier series for functions on a sphere.
They are indexed by:
- Degree (l): controls the frequency (higher means more detail)
- Order (m): varies from
-lto+l
Example Levels:
- SH level 0 (SH0): Only constant color (no view dependence)
- SH level 1 (SH1): Basic directional lighting (like Lambertian)
- SH level 2 or 3+: Captures more complex angular dependencies
🔸 SH in Gaussian Splatting
Each 3D Gaussian stores:
- Position, scale, rotation, opacity
- Spherical Harmonics coefficients for RGB appearance
Instead of storing just a single RGB color, we store a set of SH coefficients per color channel. When rendering:
- Compute the viewing direction
vfor each Gaussian. - Evaluate the SH basis functions at direction
vto get a vectorSH_basis(v). - Compute the final color as a dot product:
color = Σ (c_i * SH_basis_i(v)) for i = 1..n
where c_i are SH coefficients.
🔸 SH Level Examples
| SH Level | # Coefficients (per color) | What it Captures |
|---|---|---|
| 0 | 1 | Constant color |
| 1 | 4 | Directional diffuse lighting |
| 2 | 9 | Soft shadows, simple specular |
| 3 | 16 | Rich angular detail |
So if SH=2:
- You store 9 SH coefficients per color channel (27 total for RGB).
- You can model how color changes with view angle in a smooth and efficient way.
🔸 Visual Example (Simplified)
Imagine a glossy red ball:
- Without SH (SH=0): The ball is flat red from all directions.
- With SH=1: The ball appears brighter on the side facing the light source.
- With SH=2+: The ball has soft reflections and looks more realistic as you move the camera.
🔸 Dummy Python Code Example
import numpy as np
from scipy.special import sph_harm
# Dummy view direction (theta, phi) in spherical coordinates
theta = np.pi / 4 # angle from z-axis
phi = np.pi / 3 # angle from x-axis in x-y plane
# Compute SH basis up to degree l=2
def compute_sh_basis(theta, phi, l_max=2):
basis = []
for l in range(l_max + 1):
for m in range(-l, l + 1):
Y_lm = sph_harm(m, l, phi, theta).real # Only real part used in graphics
basis.append(Y_lm)
return np.array(basis)
# Example SH coefficients for RGB (assuming SH2 = 9 coeffs per channel)
sh_coeffs_r = np.random.rand(9)
sh_coeffs_g = np.random.rand(9)
sh_coeffs_b = np.random.rand(9)
# Evaluate SH basis
sh_basis = compute_sh_basis(theta, phi)
# Final RGB color (dot product of SH coefficients and SH basis)
r = np.dot(sh_coeffs_r, sh_basis)
g = np.dot(sh_coeffs_g, sh_basis)
b = np.dot(sh_coeffs_b, sh_basis)
print(f"RGB color from SH: R={r:.2f}, G={g:.2f}, B={b:.2f}")
This code shows:
- How SH basis functions are computed using
scipy.special.sph_harm - How SH coefficients are applied to compute view-dependent color
🔸 Summary
In Gaussian Splatting, Spherical Harmonics:
- Encode how color/appearance changes with view direction
- Provide a compact way to achieve realistic rendering
- Are used per-splat (each Gaussian has its own SH coefficients)
You can trade off quality vs speed by choosing the SH level (e.g., SH=0 for fast rendering, SH=2+ for better realism).
