Placing Gaussians Splats On Mesh Surface
In recent years, 3D Gaussian Splatting (GS) has emerged as a powerful technique for photorealistic avatar rendering and animation. Optimizing Gaussian splats without any geometric prior is challenging, as they often fail to regress accurate geometry. However, when the geometry of the object is known, fitting a mesh in advance and using its surface as a geometric prior provides a significant advantage. For example, if the object to be reconstructed is a human head, leveraging the FLAME mesh model as a geometric prior can greatly improve results.
After fitting the FLAME model, we obtain a reasonable geometric surface on which to place GSs. At this stage, how we distribute the GSs on the mesh becomes an important problem. Using a smart strategy to place the GSs on the surface can significantly aid the subsequent GS optimization process.
Naïve Random Sampling
As a baseline, GSs can be randomly distributed across the mesh surface. However, this naive approach often leads to clustering, irregular spacing, and oversampling, which degrades both visual quality and optimization stability.
Poisson Disk Sampling
To avoid the performance degradations of random sampling, Poisson Disk Sampling — a technique that enforces a minimum distance between sampled points — to robustly distribute Gaussians on the FLAME mesh.
Poisson Disk Sampling Algorithm (Bridson’s Algorithm):
- Initialize a grid with cell size = r/√2 (where r is minimum distance)
- Start with a random initial point, add to active list
- While active list is not empty:
- Pick random point from active list
- Generate k candidates (typically k=30) in annulus [r, 2r]
- For each candidate:
- Check if it’s far enough from all neighbors
- If valid, add to output and active list - If no valid candidates found, remove point from active list
Key Properties:
- Guarantees minimum distance r between all points
- Maximum distance approximately 2r
- O(n) time complexity
- Produces uniform, organic-looking distributions
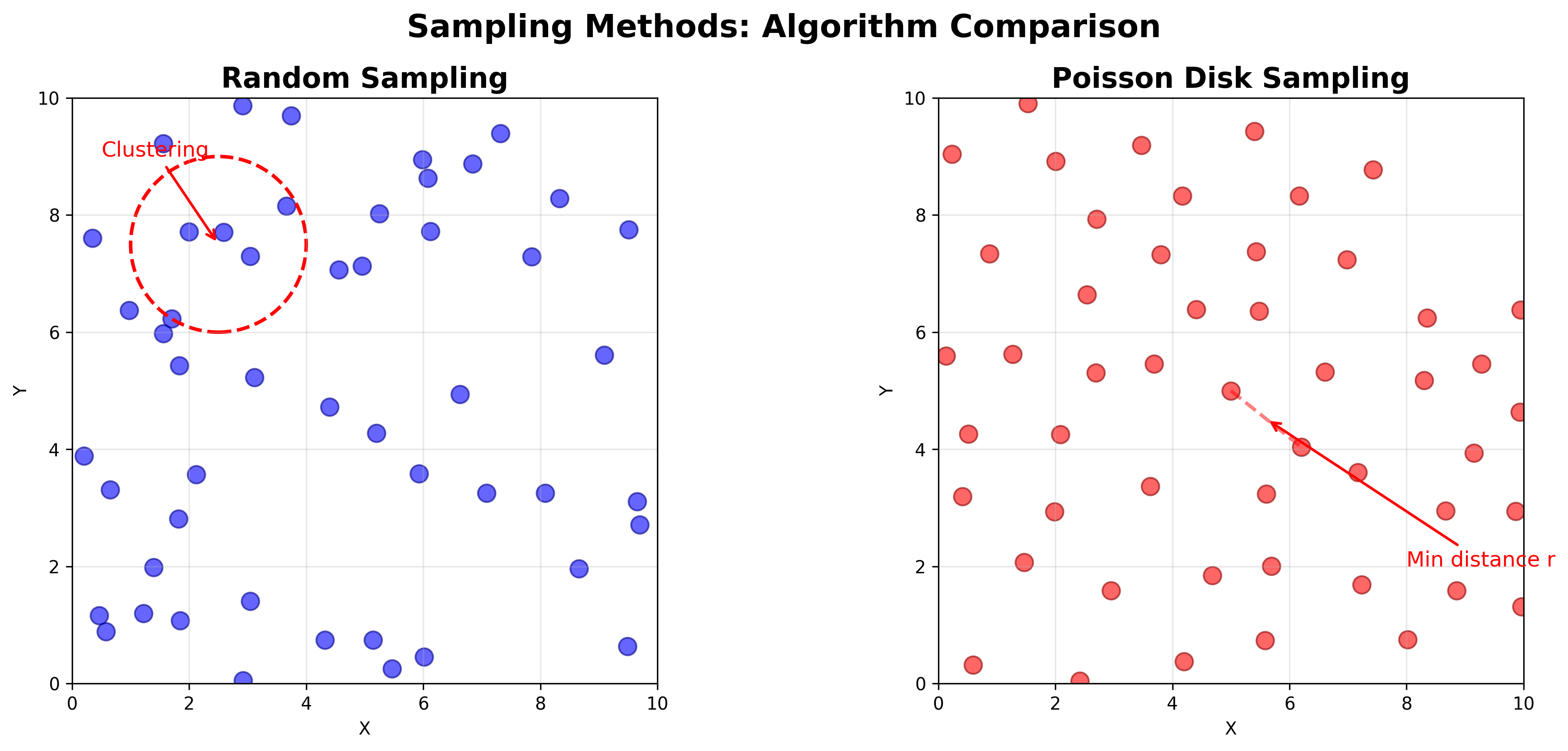
Figure 1: A side-by-side comparison of random sampling (left) and Poisson disk sampling (right) on a 2D surface.
Figure 1 shows the comparison between the two sampling methods, highlighting how Poisson Disk Sampling achieves more consistent nearest neighbor distances (lower standard deviation) and avoids extreme clustering (higher minimum distance) compared to random sampling.
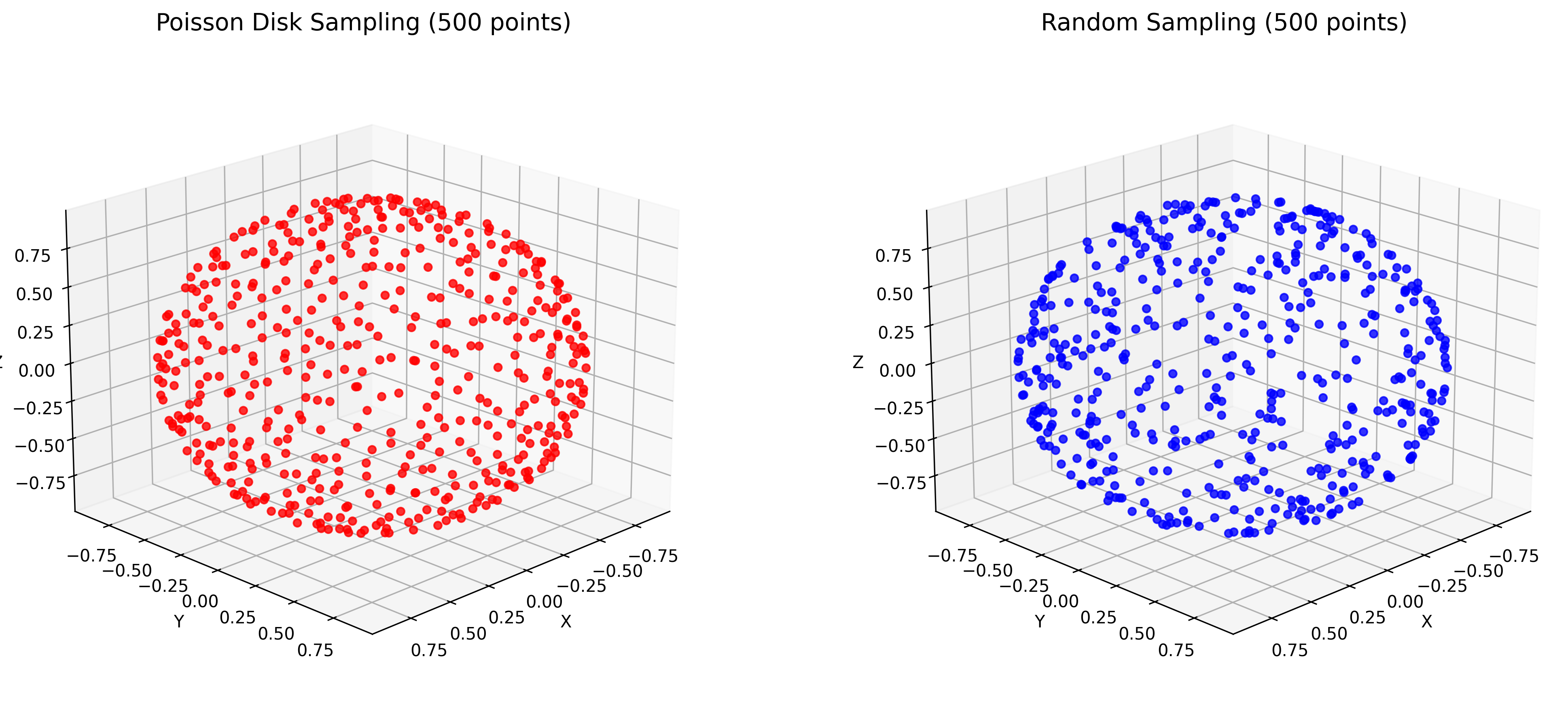
Figure 2: Comparison between random sampling (left) and Poisson disk sampling (right) on a sphere surface.
As Figure 2 shows, Poisson disk sampling provides significantly better surface coverage compared to random sampling. The uniform distribution of sample points ensures that no regions of the mesh are left sparsely covered, while simultaneously preventing overcrowding in other areas. This improved coverage translates directly to more consistent Gaussian placement across the entire FLAME mesh surface, resulting in better geometric representation and more stable optimization during the 3D Gaussian splatting process.
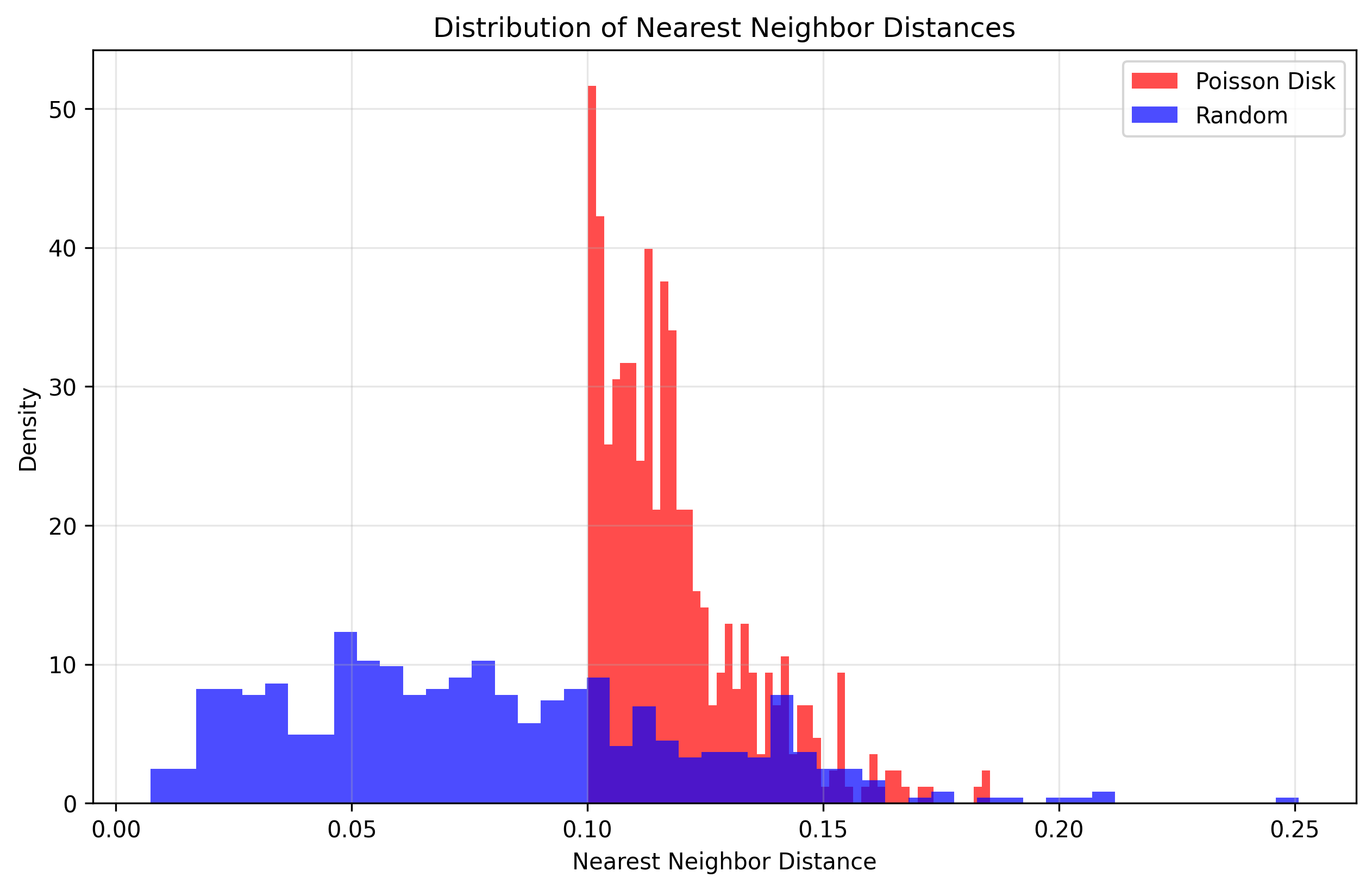
Figure 3: Nearest neighbor distance distributions for different samplings on sphere surface.
| Metric | Poisson Disk Sampling | Random Sampling |
|---|---|---|
| n_points | 500 | 500 |
| nn_mean | 0.1187 | 0.0787 |
| nn_std | 0.0160 | 0.0418 |
| nn_min | 0.1001 | 0.0073 |
| nn_max | 0.1853 | 0.2509 |
Table 1: Nearest neighbor distance statistics comparison between Poisson Disk Sampling and Random Sampling methods.
The quantitative analysis in Table 1 and the distribution visualization in Figure 3 clearly demonstrate the superiority of Poisson Disk Sampling over random sampling. Most notably, Poisson Disk Sampling maintains a significantly higher minimum distance (0.1001 vs 0.0073), preventing the extreme clustering that occurs with random sampling. The lower standard deviation (0.0160 vs 0.0418) indicates much more consistent spacing between neighboring Gaussians, while the constrained maximum distance (0.1853 vs 0.2509) ensures no large gaps in coverage. This uniform distribution is crucial for stable 3D Gaussian Splatting optimization, as it prevents both overcrowded regions that cause rendering artifacts and sparse areas that miss geometric detail.
Sampling on FLAME mesh
Figures 2 and 3 illustrate performance on a spherical surface with a more uniform geometry. In real-world applications, geometry is far from trivial—the FLAME human head mesh is both highly realistic and sufficiently complex. We will evaluate the sampling methods’ performance on the FLAME model.
Figure 4: Nearest neighbor distance distributions for different samplings.
Figure 4 visually compares random and Poisson disk sampling on the FLAME mesh for different point counts. Poisson disk sampling (bottom row, red) produces a much more uniform and evenly spaced distribution of points across the surface, as reflected by higher uniformity scores. In contrast, random sampling (top row, blue) results in visible clustering and uneven coverage, regardless of the number of points. This demonstrates that Poisson disk sampling maintains consistent regularity and superior surface coverage.
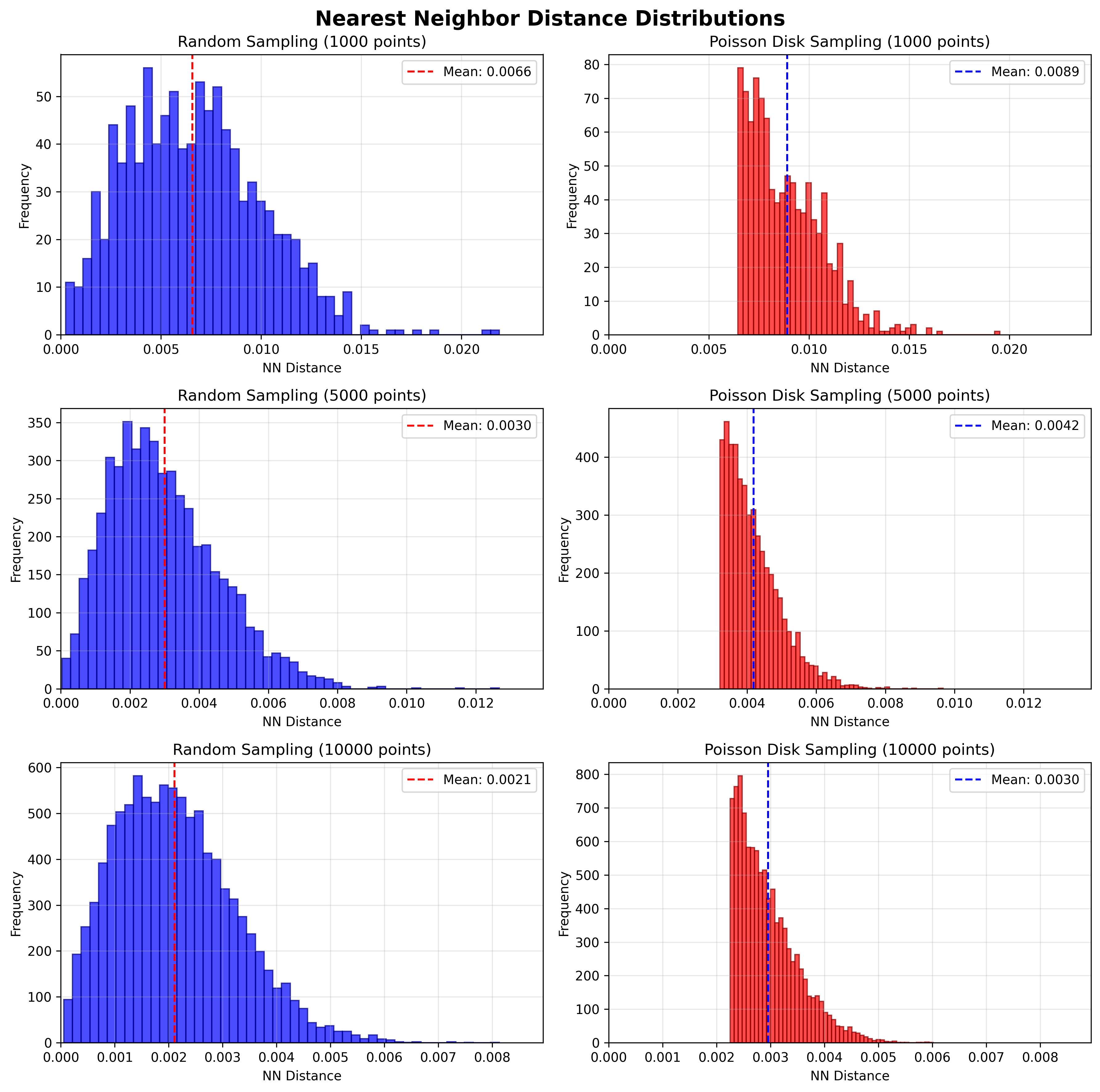
Figure 5: Nearest Neihbor distance distribution of different sampling experiments.
In Figure 5, Poisson disk sampling consistently enforces a minimum distance between neighboring samples, as shown by the sharp cutoff on the left side of each distribution. This property prevents samples from clustering too closely or overlapping, resulting in a more uniform and controlled distribution across the surface. In contrast, random sampling produces a broader spread of nearest neighbor distances, with many samples packed very closely together, leading to potential overlaps and uneven coverage. As the number of points increases, Poisson sampling maintains this regularity, while random sampling continues to exhibit significant variability and clustering. This highlights the robustness of Poisson disk sampling for applications requiring uniform coverage.
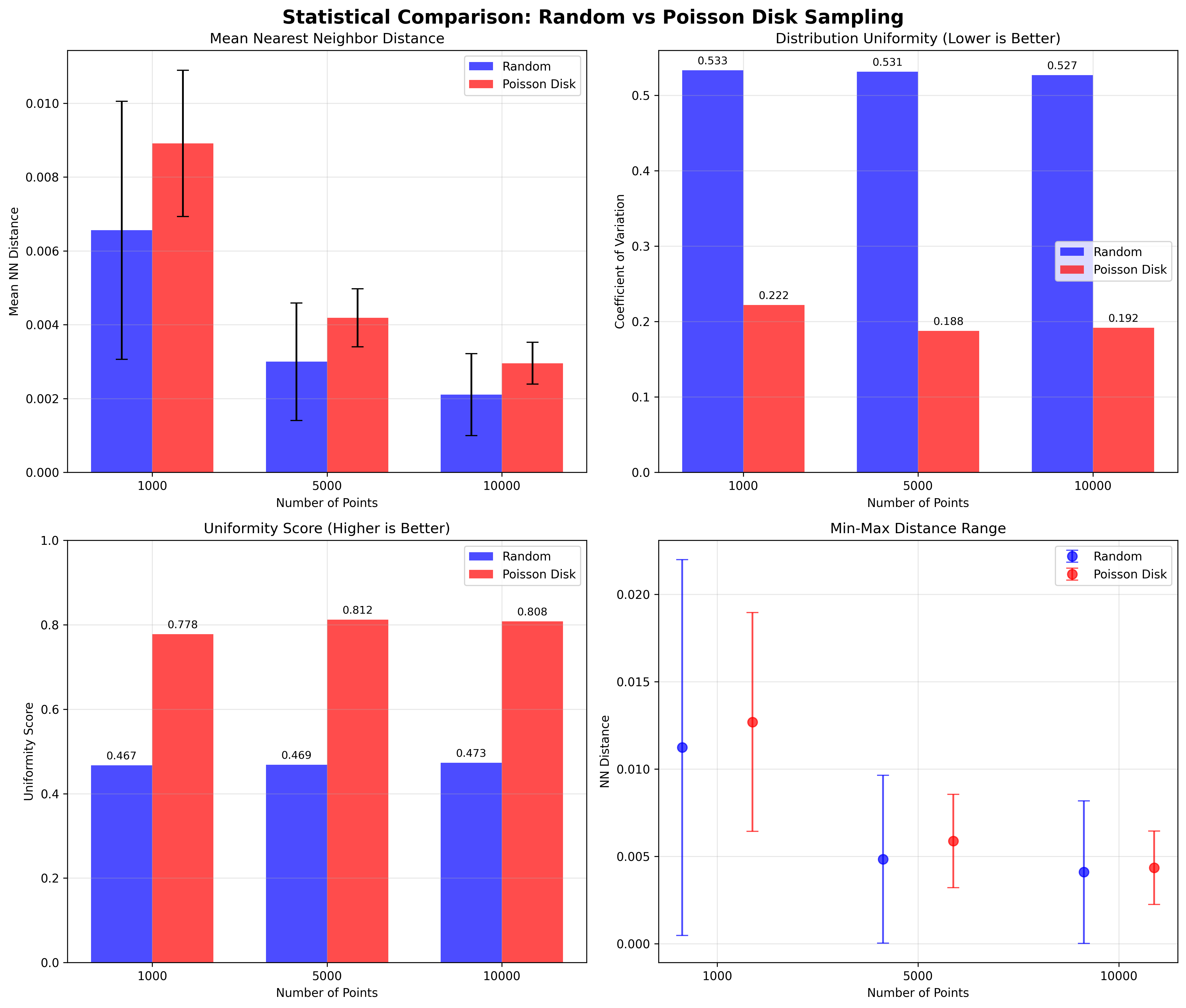
Figure 6: flame_sampling_statistics.png.
The Uniformity Score is a metric that quantifies how evenly points are distributed in a sampling. It is calculated as 1 minus the coefficient of variation (CV) of the nearest neighbor distances, where CV is the standard deviation divided by the mean. A score closer to 1 indicates a more uniform (evenly spaced) distribution, while a lower score means greater variability and less uniformity. This makes it easy to compare different sampling methods: for example, Poisson disk sampling yields higher uniformity scores than random sampling, reflecting its more consistent spacing between points.
| Points | Random Sampling | Poisson Disk Sampling |
|---|---|---|
| 1000 | 0.4906 | 0.7752 |
| 5000 | 0.4760 | 0.8107 |
| 10000 | 0.4795 | 0.8086 |
Table 2: Uniformity scores (higher is better) for random and Poisson disk sampling at different point counts.
Table 2 clearly shows that Poisson disk sampling consistently achieves much higher uniformity scores than random sampling across all point counts. This indicates that Poisson disk sampling produces a more evenly spaced and regular distribution of points on the mesh surface, while random sampling results in greater variability and less uniform coverage. The higher uniformity of Poisson disk sampling is especially important for applications that require consistent surface representation and stable optimization.
Conclusion
For placing Gaussians on mesh surfaces, uniform coverage, minimal overlap, adaptive density, and mesh-awareness are essential. Naïve random sampling often leads to clustering, gaps, and unstable optimization. In contrast, Poisson Disk Sampling enforces even spacing and respects mesh geometry, resulting in a more regular and robust distribution. Having better geometric priors at the start of Gaussian splat optimization leads to more accurate and consistent recovery of visual details. This approach enables more accurate and stable neural avatar representations, improving rendering quality and optimization convergence—especially for complex models and advanced techniques such as GEM, RGBAvatar, or 3D Gaussian Blendshapes.
